Homomorphic-Encryption Accelaration Architectures
Many modern computing devices operate under strict constraints in power, storage, and processing capacity. To achieve full functionality, they often rely on cloud services for offloading computation. However, this dependency introduces significant privacy risks, as sensitive data is frequently stored and processed in shared cloud environments.
Homomorphic encryption (HE) offers a promising solution by enabling secure computation directly on encrypted data, preserving privacy throughout the process. Despite over a decade of advancements that have improved its practicality, HE remains computationally intensive—often several orders of magnitude slower than conventional methods, making it prohibitively expensive and impractical for applications such as medical devices.
Current processor architectures are not optimized to meet the computational demands of Fully Homomorphic Encryption (FHE), particularly in privacy-critical domains. Addressing this challenge requires purpose-built hardware solutions. As part of our research, we are developing a configurable lattice-based cryptographic processor using a modular, library-driven approach built around Ring-Learning with Errors (RLWE) homomorphic encryption primitives.
Traditional platforms such as x86-64 CPUs, GPUs, and FPGAs introduce significant overhead, making homomorphic encryption prohibitively slow, inefficient, and costly, especially for targeted applications like secure medical devices and edge computing. Our objective is to deliver a specialized architecture that achieves an order-of-magnitude performance improvement over existing solutions, enabling practical and scalable deployment of homomorphic encryption.
Background
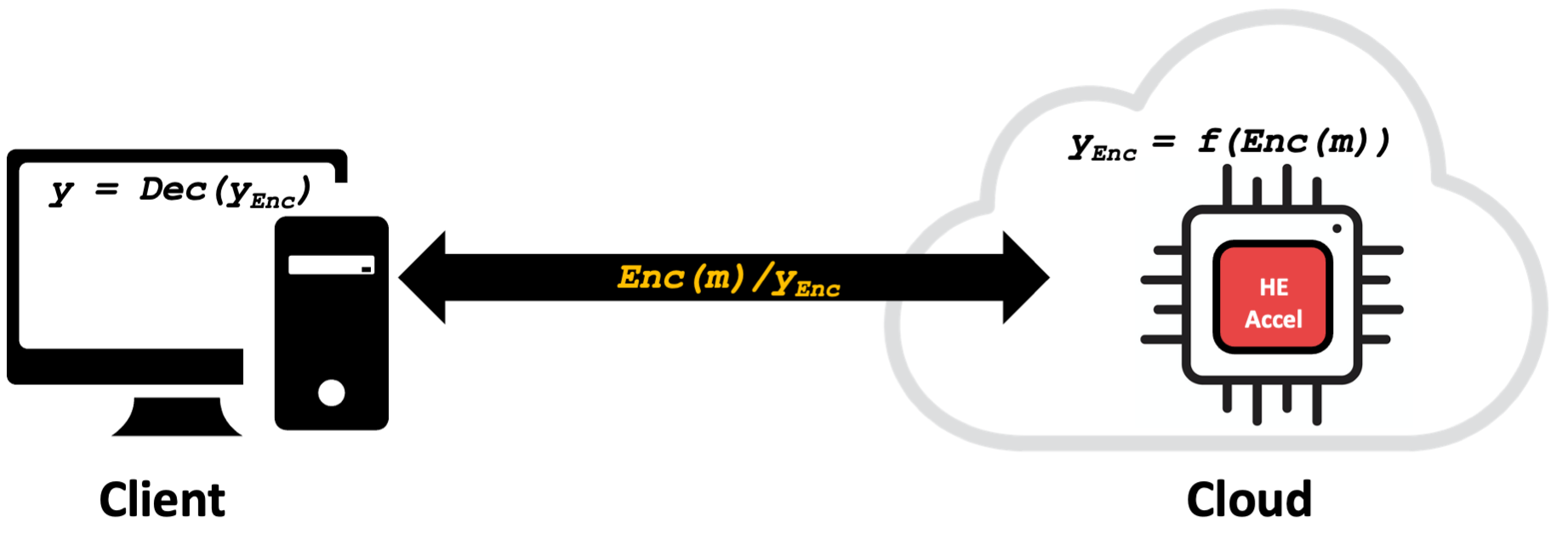
Homomorphic encryption is a transformative cryptographic technique that enables secure cloud-based storage and computation. It allows mathematical operations to be performed directly on encrypted data, producing encrypted results that, once decrypted by the data owner, match the outcome of the same operations on plaintext.
This capability ensures that sensitive data can be processed in the cloud without ever being exposed. The data owner encrypts the information locally and sends it to the cloud, where computations are performed without access to the underlying data or private keys. The encrypted results are then returned to the data owner, who decrypts them using their private key. This process effectively mitigates privacy risks associated with cloud computing by ensuring that the cloud provider never sees the raw data.
The concept of homomorphic encryption was first introduced by Rivest et al. in 1978. It wasn’t until 2009 that Craig Gentry’s groundbreaking work provided a viable framework for fully homomorphic encryption (FHE), marking a turning point in the field. Over the past decade, significant progress has been made to improve its practicality. However, despite these advancements, homomorphic encryption remains computationally intensive, often several orders of magnitude slower than conventional methods, making it costly and resource-demanding for large-scale deployment.
To address these limitations, extensive efforts have been directed toward developing robust software libraries for homomorphic encryption. Notable examples include SEAL, Palisade, cuHE, HElib, NFLLib, Lattigo, and HEAAN. These libraries are built on Ring-Learning with Errors (RLWE) cryptographic foundations and typically implement schemes such as Brakerski-Gentry-Vaikuntanathan (BGV), Fan-Vercauteren (FV), and Cheon-Kim-Kim-Song (CKKS), all of which share similar parameter structures.
Design Methodology
Given the rapidly evolving landscape of homomorphic encryption (HE) schemes, our design philosophy emphasizes flexibility and adaptability. Rather than optimizing hardware for a single algorithm, we’ve developed a modular hardware suite that supports the core operations shared across diverse HE approaches. This includes foundational capabilities for lattice-based computations, polynomial arithmetic, logical operations, statistical sampling, and finite field processing. This architecture enables researchers and developers to experiment with emerging HE designs while maintaining a robust and reusable hardware foundation.
Large Arithmetic Word Size (LAWS)
Word size plays a critical role in determining the signal-to-noise ratio (SNR) during ciphertext storage and computation in homomorphic encryption. Currently, no mainstream hardware architecture natively supports the register widths or execution units required for the fundamental mathematical and logical operations in lattice-based FHE schemes. Conventional platforms exacerbate this issue: x86 architectures are limited to 64-bit registers, while GPUs typically operate on 16- or 32-bit operands. These legacy constraints, designed for entirely different computational paradigms, introduce significant overhead when executing FHE workloads, which ideally require registers and operators that span thousands of bits.
To overcome this limitation, we are developing a specialized architecture called LAWS (Lattice Arithmetic Word System), purpose-built to support the wide-word operations essential for efficient FHE computation on modern hardware.
ISA Informed by FHE Mathematical Operations
This design methodology aims to establish an instruction set architecture (ISA) grounded in the core mathematical operations essential to fully homomorphic encryption (FHE) schemes. It is informed by ongoing research into optimizing FHE algorithms. A major computational bottleneck across nearly all known FHE schemes is the extensive use of finite field arithmetic. Additionally, the frequent sampling from complex statistical distributions presents further performance challenges. Our approach addresses these concerns by building hardware support for these foundational operations, enabling broader algorithmic compatibility and future-proofing against evolving cryptographic techniques.
ISA Based Reconfigurable Architecture
As homomorphic encryption (HE) continues to evolve, even the long-term viability of recently standardized algorithms remains uncertain. Therefore, our design strategy emphasizes both adaptability and performance. Instead of optimizing hardware for a single scheme, we are building a platform that accelerates lattice-based FHE while enabling experimentation with emerging cryptographic designs. This flexibility is achieved through a comprehensive instruction set that supports essential operations—including lattice arithmetic, polynomial processing, logical computation, and finite field manipulation—providing a robust foundation for innovation across diverse HE frameworks.
Fast Arithmetic Hardware Library For RLWE-Based Algorithms
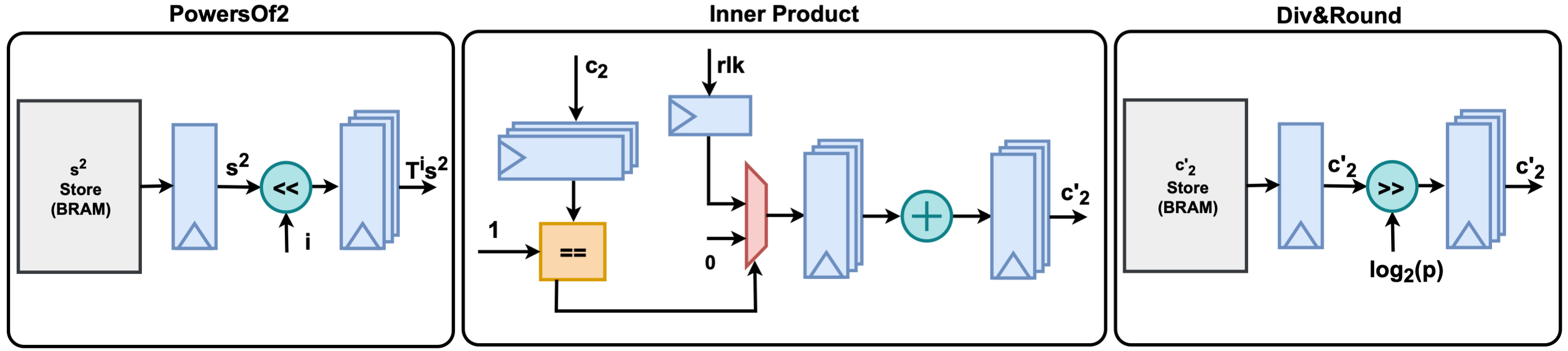
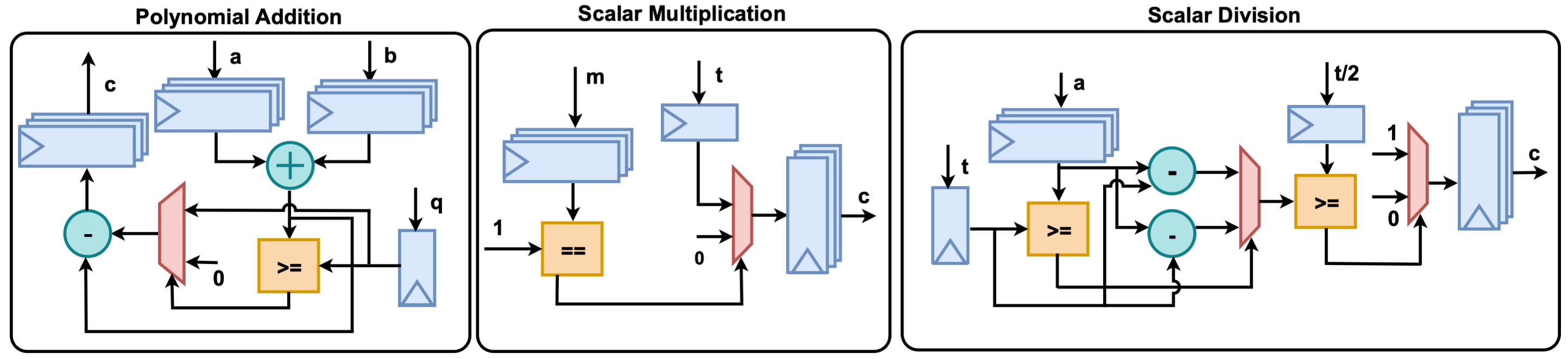
Using our methodology, we have developed a first-of-its-kind open-source arithmetic hardware library specifically designed to accelerate the core operations of Ring Learning with Errors (RLWE)-based homomorphic encryption (HE).
This hardware accelerator includes modular components for:
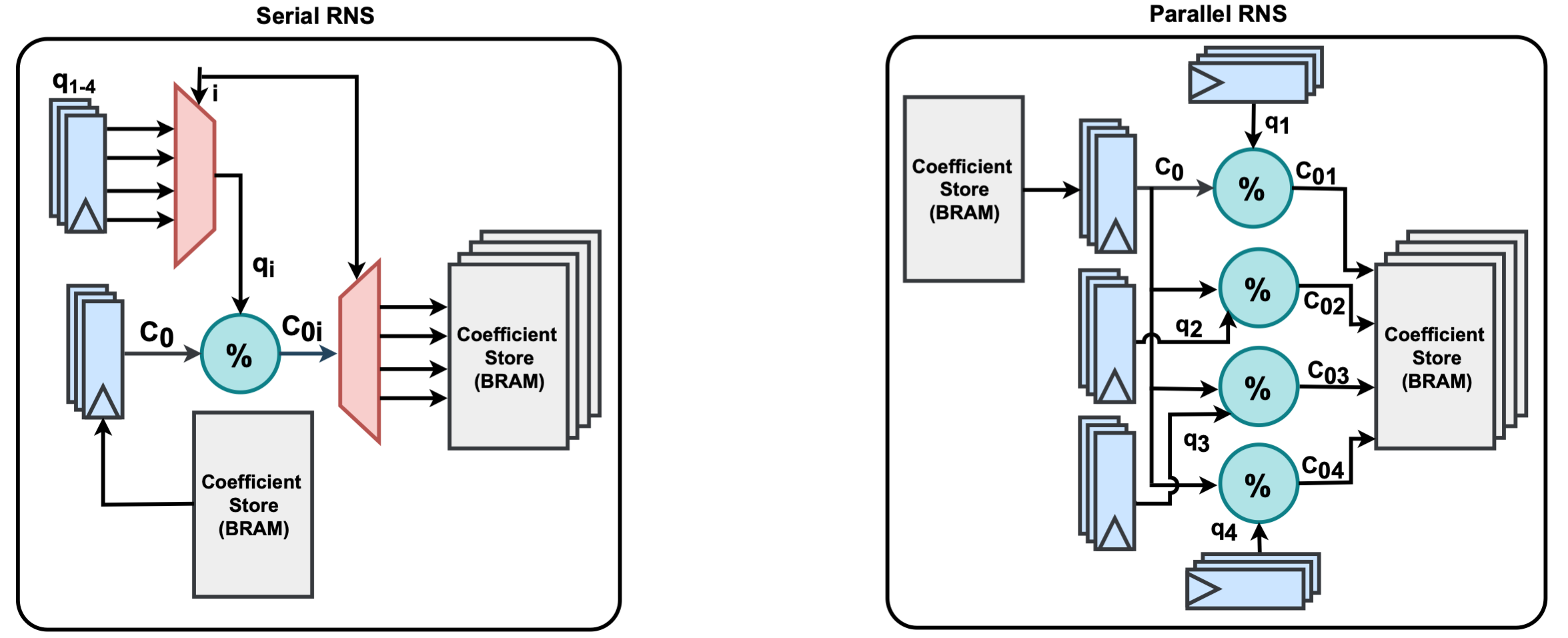
- Residue Number System (RNS)
- Chinese Remainder Theorem (CRT)
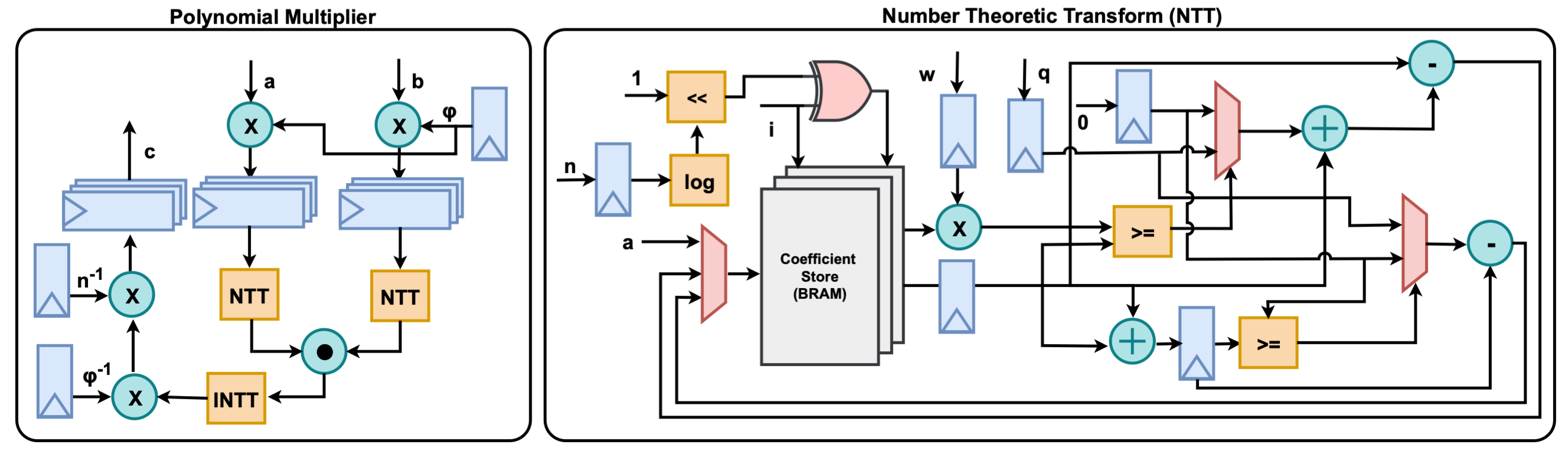
- NTT-based polynomial multiplication
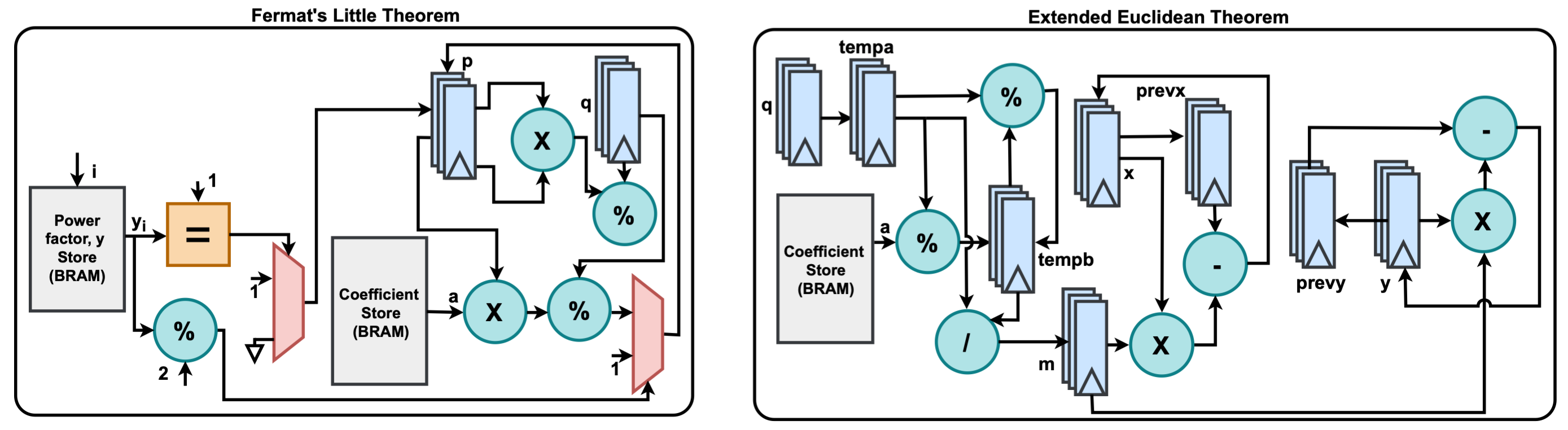
- Modulo inverse and reduction
- Polynomial and scalar arithmetic.
Each operation is implemented with both serial (cost-efficient) and parallel (high-performance) variants wherever feasible. The library follows a modular and parameterized design approach, allowing easy customization and extensibility for a wide range of HE applications, particularly those targeting FPGA-equipped cloud infrastructures.
Using the submodules from the library, we prototyped a hardware accelerator on FPGA. Performance evaluations show dramatic improvements: approximately 4200x speedup for homomorphic multiplication and 2950x for homomorphic addition compared to existing software implementations.
Candidate Architecture Design
HERISCV (Homomorphic Encryption-Enabled RISC-V) is a specialized accelerator architecture built on the RISC-V instruction set, designed to support the core arithmetic operations fundamental to Ring Learning with Errors (RLWE)-based homomorphic encryption. It introduces native ISA-level support for key submodules, including Residue Number System (RNS), Chinese Remainder Theorem (CRT), NTT-based polynomial multiplication, modulo inverse, modulo reduction, and the other polynomial and scalar operations.
To validate the HERISCV architecture, we are applying it to accelerate Signal Processing in the Encrypted Domain (SPED), with a particular focus on optimizing core linear algebra kernels under encryption constraints.
Hardware Downloads
Authors
PQC Secure is a collaborative initiative between the cryptography team at Secure Micro Technologies and the Secure, Trusted, and Assured Microelectronics (STAM) Center at Arizona State University’s Ira A. Fulton Schools of Engineering.
Copyright ©. All Rights Reserved — Secure Micro Technologies